You cannot select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
11 months ago | |
|---|---|---|
| Readme_files | 11 months ago | |
| .gitignore | 12 months ago | |
| Readme.md | 11 months ago | |
| main.ipynb | 11 months ago | |
Readme.md
#!pip3 install tensorflow
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# data for training the ann mode
# option 1:
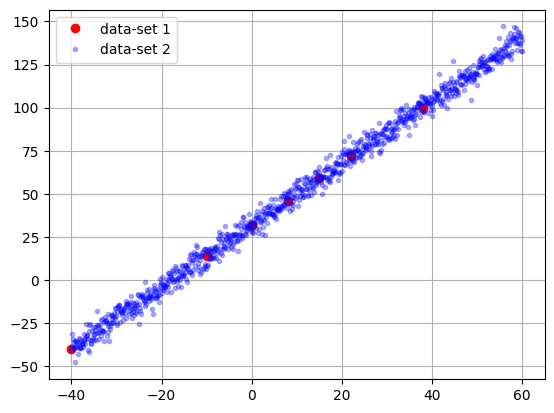
celsius = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float)
fahrenheit = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float)
# option 2: (X°C x 9/5) + 32 = 41 °F
points = 1000
np.random.seed(99)
dataIn = np.linspace (-40,60, points)
target = dataIn*9/5 + 32 +4*np.random.randn(points)
plt.plot(celsius, fahrenheit, 'or', label='data-set 1')
plt.plot(dataIn, target, '.b', alpha=0.3, label='data-set 2')
plt.legend()
plt.grid()
plt.show()
from tensorflow.keras.models import Sequential # ANN type
from tensorflow.keras.layers import Dense, Input # All nodes connected
# NN definition
hn=2
model = Sequential()
model.add(Input(shape=(1,), name='input'))
model.add(Dense(hn, activation='linear', name='hidden'))
model.add(Dense(1, activation='linear', name='output'))
model.summary()
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ hidden (Dense) │ (None, 2) │ 4 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ output (Dense) │ (None, 1) │ 3 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 7 (28.00 B)
Trainable params: 7 (28.00 B)
Non-trainable params: 0 (0.00 B)
### veri important note implement a python code
# to show the ANN model connection using ascii
from tensorflow.keras.optimizers import Adam
#hyper parameters
epoch = 500
lr = 0.01
tf.random.set_seed(99) # For TensorFlow
model.compile(optimizer=Adam(lr), loss='mean_squared_error')
print("Starting training ...")
historial = model.fit(dataIn, target, epochs=epoch, verbose=False,)
print("Model trainned!")
Starting training ...
Model trainned!
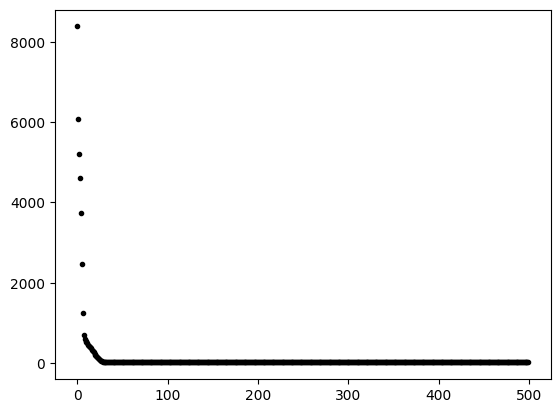
plt.plot(historial.epoch, historial.history['loss'], '.k' )
plt.show()
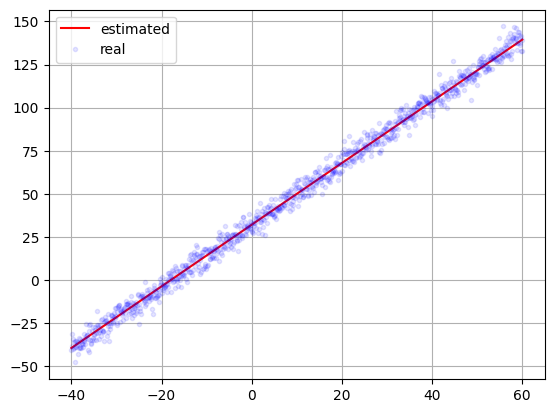
predict = model.predict(dataIn)
plt.plot(dataIn, predict, '-r', label='estimated')
plt.plot(dataIn,target, '.b', label='real', alpha=0.1)
#plt.xlim([0, 20])
#plt.ylim([32, 39])
plt.legend()
plt.grid()
plt.show()
[1m32/32[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 741us/step
for layer in model.layers:
print(layer.get_weights())
[array([[ 0.7760521 , -0.18955402]], dtype=float32), array([8.428659, 8.034532], dtype=float32)]
[array([[2.4613197 ],
[0.63733613]], dtype=float32), array([6.2560296], dtype=float32)]
# Get weights
for layer in model.layers:
weights = layer.get_weights()
print(f"Layer: {layer.name}")
print(f" Weights (Kernel): {weights[0].shape} \n{weights[0]}")
print(f" Biases: {weights[1].shape} \n{weights[1]}")
Layer: hidden
Weights (Kernel): (1, 2)
[[ 0.7760521 -0.18955402]]
Biases: (2,)
[8.428659 8.034532]
Layer: output
Weights (Kernel): (2, 1)
[[2.4613197 ]
[0.63733613]]
Biases: (1,)
[6.2560296]
inData = np.array([100])
model.predict(inData)
[1m1/1[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 25ms/step
array([[211.05261]], dtype=float32)
wih = np.array([[ 0.7760521, -0.18955402]])
bh = np.array([8.428659, 8.034532])
Xh = np.dot(inData, wih) + bh
who = np.array([[2.4613197 ],[0.63733613]])
bo = np.array([6.2560296])
O = np.dot(Xh,who) + bo
O
array([211.05262121])
Testing the model
inTest = np.array([100])
model.predict(inTest)
[1m1/1[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 22ms/step
array([[115.929985]], dtype=float32)
# Do the Maths:
inTest = np.array(inTest)
whi = np.array([[-0.27738443, 0.7908125 ]])
bh = np.array([-8.219968, 6.714554])
Oh = np.dot(inTest,whi)+bh
who = np.array([[-1.9934888],[ 1.5958738]])
bo = np.array([5.1361823])
Oo = np.dot(Oh,who)+bo
Oo
array([213.73814765])
sklearn
from sklearn.neural_network import MLPRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import numpy as np
# Datos de ejemplo
# Escalado de los datos
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_scaled = scaler_X.fit_transform(dataIn.reshape(-1,1))
y_scaled = scaler_y.fit_transform(target.reshape(-1, 1)).ravel()
# Modelo equivalente al de Keras
mlp = MLPRegressor(
hidden_layer_sizes=(2,), # 1 capa oculta con 2 neuronas
activation='identity', # activación lineal
learning_rate_init=0.001, # 👈 Learning rate
solver='adam',
max_iter=1000,
tol=1e-6,
random_state=4
)
# Entrenar modelo
mlp.fit(X_scaled, y_scaled)
# Predicción
y_pred_scaled = mlp.predict(X_scaled)
y_pred = scaler_y.inverse_transform(y_pred_scaled.reshape(-1, 1))
# Visualizar resultados (opcional)
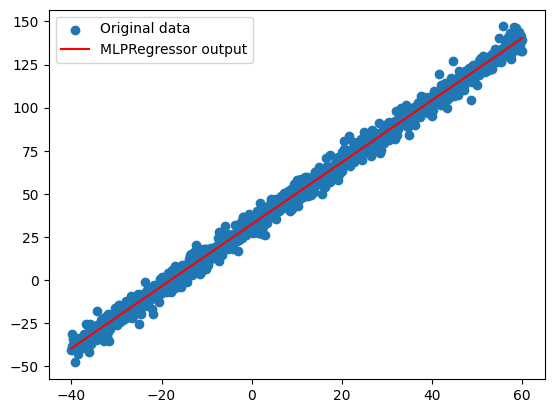
import matplotlib.pyplot as plt
plt.scatter(dataIn, target, label="Original data")
plt.plot(dataIn, y_pred, color='red', label="MLPRegressor output")
plt.legend()
plt.show()
plt.plot(mlp.loss_curve_,'.k')
plt.xlabel("Épocas")
plt.ylabel("Error (loss)")
plt.title("Evolución del error en entrenamiento")
plt.grid(True)
plt.show()
print("Pesos entre capa de entrada y oculta:", mlp.coefs_[0])
print("Pesos entre capa oculta y salida:", mlp.coefs_[1])
print("Bias de capa oculta:", mlp.intercepts_[0])
print("Bias de salida:", mlp.intercepts_[1])
Pesos entre capa de entrada y oculta: [[ 1.70549238 -0.37235861]]
Pesos entre capa oculta y salida: [[ 0.30934654]
[-1.25842791]]
Bias de capa oculta: [1.02819949 1.02732046]
Bias de salida: [0.97683886]
Model scheme
def generate_ascii_ann(model):
ascii_diagram = "\nArtificial Neural Network Architecture:\n"
for i, layer in enumerate(model.layers):
weights = layer.get_weights()
# Determine layer type and number of neurons
if isinstance(layer, Dense):
input_dim = weights[0].shape[0] # Number of inputs
output_dim = weights[0].shape[1] # Number of neurons
ascii_diagram += f"\nLayer {i+1}: {layer.name} ({layer.__class__.__name__})\n"
ascii_diagram += f" Inputs: {input_dim}, Neurons: {output_dim}\n"
ascii_diagram += f" Weights Shape: {weights[0].shape}\n"
if len(weights) > 1: # If bias exists
ascii_diagram += f" Biases Shape: {weights[1].shape}\n"
# ASCII representation of neurons
ascii_diagram += " " + " o " * output_dim + " <- Output Neurons\n"
ascii_diagram += " | " * output_dim + "\n"
ascii_diagram += " " + " | " * input_dim + " <- Inputs\n"
return ascii_diagram
# Generate and print the ASCII diagram
ascii_ann = generate_ascii_ann(model)
print(ascii_ann)
Artificial Neural Network Architecture:
Layer 1: hidden (Dense)
Inputs: 1, Neurons: 2
Weights Shape: (1, 2)
Biases Shape: (2,)
o o <- Output Neurons
| |
| <- Inputs
Layer 2: output (Dense)
Inputs: 2, Neurons: 1
Weights Shape: (2, 1)
Biases Shape: (1,)
o <- Output Neurons
|
| | <- Inputs
graph LR
I1((I_1)) --> H1((H_1)) & H2((H_1))
H1 & H2 --> O1((O_1)) & O2((O_2))